Leibniz developed the d/dx notation for derivative--which is important, in part because it makes things like the chain rule make sense:
It looks like the "with respect to 'u' " cancels with the "differential of 'u' " by fraction multiplication, which makes it less awkward than Newton's notation of putting a dot over the variable to be differentiated, equivalent to modern prime notation. It also allows for a more subtle definition of the derivative. For example, what if you are trying to derive a function like
z = sin(x)sin(y)
which represents a surface? Newton's notation would suggest that
ż = cos(x)cos(y)
but this does not, in fact, make any sense. What does it mean, say, that the "slope" of this surface at (x=0,y=0)=cos(0)sin(0)=1? Geometrically, it has no real relationship to the graph, nor does it have any algebraic meaning. Leibniz's notation lets us make sense of it. For him, we have to take the derivative with respect to a variable, so to take the derivative of z, we have dz/dx = cos(x)sin(y) or dz/dy = sin(x)cos(y). Now we have some statements that do make sense: the derivative with respect to x is the change in z over x with constant y--the slope of the tangent line to the surface parallel to the plane y=0--and the same is true of the derivative with respect to y and the plane x=0. This seems sort of abstruse or gimmicky, but it is actually very useful in fields like geometry and physics. To give a brief example, you can use this concept to find the change in the volume of a cone over the radius given a certain height, or over the height of a cone given a certain radius.
The point, anyway, is that Leibniz understood much better what a derivative actually is: it represents the change in a variable given a change in a related variable. Newton understood it incompletely as meaning the change in a variable.
[No more calculus past this point.]
Leibniz also made some considerable contributions to physics. His theory of "monads", while more a philosophical tool than a scientific theory, presupposed the existence of distinct elements of matter. He also formulated an early definition of kinetic energy, calling it the most "fundamental" and immutable of "forces", which is very similar to conservation of energy.

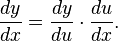

1 comment:
I knew we currently use more of Leibniz's notation than Newton's, but I was never really sure who came up with what notation. Now that you point out the differences and the advantages of Leibniz's versions, I think I understand it a lot better. Also, I had no idea that he made such significant contributions to physics as well; he must have been a true polymath to contribute to much to so many fields.
Post a Comment